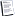
OK, Nav, its clear you're not going to get this without some help. You keep
claiming the centrifugal force varies across the Earth. However, that is not
the case. Your assumption is that the Earth is rotating around the E-M
barycenter, and that because that is offset from the Earth center, the
centrifugal force is unbalanced. (Or more precisely, you claim the "r" in the
centrifugal force equation is different on the near and far sides of the Earth.)
However, if we remove the daily rotation, the Earth does not move around the
barycenter quite like you think. Only the center of the Earth describes a
circle around the barycenter. A point on the surface rotates around a point
offset by an Earth radius towards that point. Thus, the "r" in the centrifugal
force equation is the same for all points on the Earth.
I know this is hard concept to grasp at first, but its really quite simple once
you see it. To help visualize, rub your hand around your tummy, holding it
horizontal. The center of your hand rotates around the center of your stomach,
perhaps with a two inch radius. Your fingertips will also describe a two inch
circle, offset to the side. All points on your hand will describe the same
circle, and feel the same centrifugal acceleration.
Given that, your argument falls apart. The centrifugal force is exactly the
same on all points of the Earth, and (not by coincidence) is exactly opposite
the net gravitational force. What is left over is the differential gravity.
Now that's a simple proof.
So tell us Nav, why did you chose to ignore the Sun's contribution? You deleted
my comments that following your arguments, the Sun's contribution is 1% of the
Moon's; this is clearly at variance with reality.
"Nav" wrote in message
...
Jeff Morris wrote:
So, you you're claiming the lunar tidal forces are 65 times the accepted
values.
No I'm not saying that. The tidal forces are what they are ("accepted
values?"). I can see you are very stubborn. The point is that the
outward component due to rotation is much larger than the apparent
outward force due to the change in distance and gravity. It's a fact
-you've calculated it for yourself!
Or is my equation for centrifugal acceleration wrong?
Actually, applying it in this context is your problem. Centrifugal
acceleration
is constant, it doesn't vary across the surface of the Earth as you claim.
Remember, it doesn't even exist, its actually a reference frame shift.
It is a much larger force than differential gravity but you want to
ignore it? You are wrong Jeff, it does vary across the surface of the
earth Jeff -the Barycenter is at ~3/4 r! On the moon side it's ~1/7 as
large. Finally, (repeating yet again) it is the ____DIFFERENCE______
between inertial and gravity forces that make the tides. To say it's
only "differential gravity" (I shudder at that term) is clearly wrong -
this was a simple proof.
Cheers
|