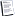
I wasn't convinced about your theory intuitively but once i jotted some
formulae down it seemed to make sense.
Power = work / time
work = force x distance

in this case resistance is equal to force and assuming a constant distance
travelled then work is proportional to resistance.
hence
2 x speed == 4 x force (resistance) == 4 x work in 0.5 x time == 4/0.5 =
8 x power
3 x speed == 9 x force (resistance) == 9 x work in 1/3 x time == 9/0.333
= 27 x power

seems like the cube function works assuming the square relationship of speed
versus resistance.

My apologies :-)

I'm glad my boat can get up on the plane.




"JAXAshby" wrote in message
...
because you need the horsepower to overcome resistence, *plus* the
horsepower
to increase speed.

Not an entirely precise statement, but "close enuf" in this discussion.

This doesn't sound right.
Why would the horsepower required go up by a factor different to the
resistance?
I would guess that power use would increase at close to the same rate as
the
resistance.





"JAXAshby" wrote in message
...
the resistence to movement of a displacement hull goes up with the
square
or
speed, and the horsepower needed goes up with the cube of speed.

so, in more or less correct terms, doubling the speed of a displacement
hull
requires about 8x the power.

Does anybody know what relation there is between fuel consumption of a
displacement hull and its speed?
Is this linear, quadratic or something else? To make it more concrete,
say you have a consumption of 60l/h at cruising speed. Would you then
e.g. see 30l/h at half the cruising speed and 15l/h at 1/4th the
cruising speed or would it be more, or less?

TIA, if you prefer (also) email amulder(AT)rootshell.be